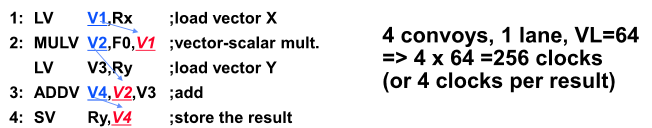Problems with conventional approach
ILP의 제약
pipelined clock rate: Clock rate를 증가해도 다른 브랜치나 해저드의 영향이 증폭되어 어느정도까지 속도에 한계에 봉착함
Fetch, decode가 어느 포인트에 도달하면 한번에 fetch decode하는 일의양이 커지기 때문에 ILP 한계점 존재
cache hit rate: 캐쉬가 다양한 데이터 특성에 따라 다양하게 성능이 발생, 많은 양의 데이터 셋은 locality가 나쁘게 동작
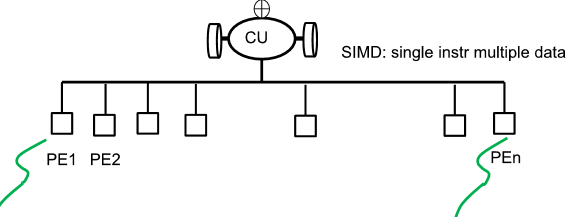
Alternative Model: Vector Processing
응용프로그램의 수행 패턴을 보면 scalar + parallel 의 결합으로 구동이 됨
CPU core + accelerator(vector, DSP, GP-GPU)
Vector - 전통적인 슈퍼컴퓨터(지금은 벡터엔진)
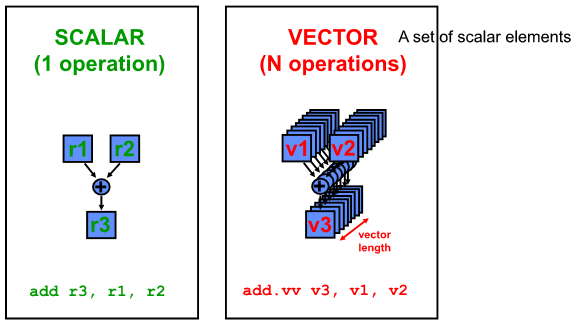
Vector 가 무엇인지?
SCALA - single data object 에 스케일 연산(단위데이터 연산)해 single 데이터를 얻어내는 것
이런 SCALAR의 집합 = VECTOR
Properties of Vector Processors
각각의 수행결과는 이전 수행 결과와 독립적이여야함
메모리 접근하는데 array 한정된 연산이라 메모리 접근이 잘 알려진 것 사용
Highly interleaved 로 하고 64개 이상의 latency 감소시켜 캐쉬도 큰 역할을 못함
한 개의 백터명령어가 64개의 element가 있다면 64개의 동작의 연산을 수행하는 것
Loop 제어를 구체적으로 해주어야하지만 이게 필요가 없어 브랜치에 의해 야기하는 문제점이 없는 특징이 있음
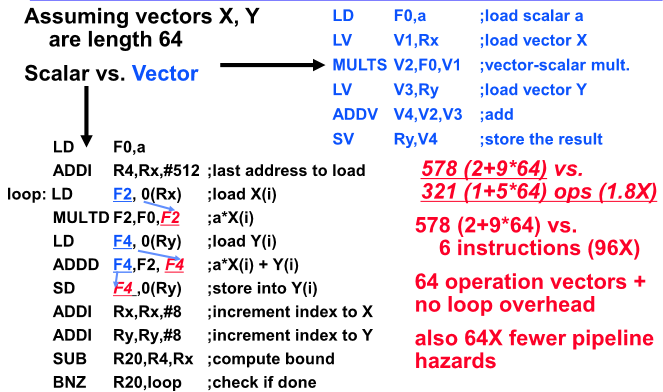
한 개의 명령어가 엄청난 일을 수행하기 때문에 똑같은 문제를 코드 구현 시 절약됨(반노이만 머신의 메모리로 부터 계속 fetch해야하는 것이 줄기때문에 상당한 효과가 있음)
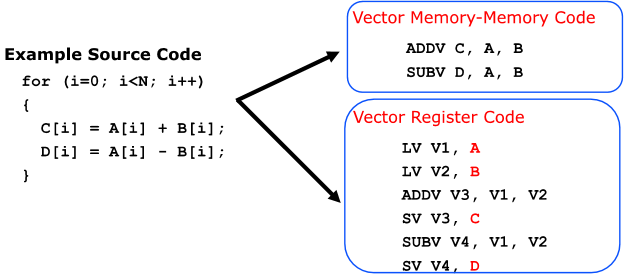
Styles of Vector Architectures
Memory-Memory Vector Processors : 모든 vector 연산인 메모리를 기본으로함
Vector-Register Processors: 모든 vector 연산이 register를 기본으로함(load, store 제외)
Vector Memory-Memory vs Vector Register
Componets of Vector Processor
Vector Register - signle vector를 저장할 수 있는 Register 필요 (2개를 동시에 읽고 하나를 쓰는 port가 필요, 8-32개 가 각각은 62-128개의 64bit로 구성됨)
Vector Functional Units(FUs): Vector 수행 엔진, pipelined 구조이고 매 사이클 마다 일련의 vector를 수행할 수 있도록 다단계로 설계함
Vector Load-Store Units: 메모리와 레지스터간 데이터 주고받을 unit 필요(주어진 vector를 빠르게 읽고 저장)
Scalar registers: 일반적인 데이터를 저장할 수 있응 모듈
Cross-bar: 이것들 모두 연결시키는 것
DLXV Vector Instruction
LVWS= Stride 간격으로 가져옴
LVI= non zero 값들만 모어서 연산을 해야할 때 사용(선형대수에 대부분 sparse matrix 임)
Memory operations
Load/Store는 레이스터 메모리간 데이터 이동하는 연산
addressing 3가지 타입
- Unit stride : 시작부터 순차적으로 읽음
- Non-unit stride : 일정한 간격으로 읽음
- Indexed(gather-scatter[연산결과를 다시 원위치에 store하는 것이 scatter]) : sparse arrays 데이터 읽을 때 좋음
DAXPY(Y=a*X+Y)
Vector Utilization
inner loop parallelism: nested loop에서 inner loop를 하나의 백터로 만들어서 사용
outer loop parallelism: column 단위로 백터를 형성할 수도 있음(프로세서가 64개가 있는 matchine 처럼 생각할 수 있음)
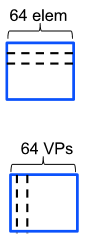
Virtual Processor Vecgtor Model
Vector 연산은 SIMD 연산임
Lanes - Mutiple parallel execution units
Vector Execution Time
Initiation rate: lanes의 개수
Convoy: 한번에 동시에 시작할 수 있는 vector 명령어의 집합
Chime: 한개의 convoy가 수행을 하는데 소요가 되는 시간
m convoys take m chimes 으로 이야기 할 수 있음
(vector length가 n이라면 m*n 사이클이 걸림)
동시에 들어갈 수 있는 것 나누면 4덩어리가 나오므로 4convoys고 vector length 가 64 dlaus 4*64 = 256 사이클이걸림
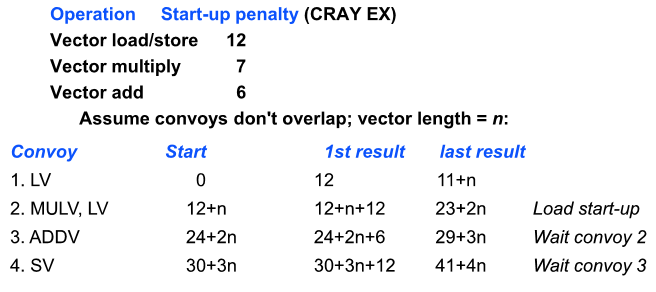
DLXV Start-up Time
파이프라인을 채우는 latency - start up time
LV 첫번째 수행결과가 12번째 나옴
이후 한개씩 결과가 나오면 vector length는 n이라고하면 n-1을 12 에 더해 11+n 결과가 나옴
2번째 convoy는 둘중에 큰 애에 따라 12+n에 시작해 첫번째 결과는 12+n+12이고 n-1을 더하면 23+2n 에 끝나게됨
쭉 가면 최종적으로 41+4n에 끝남
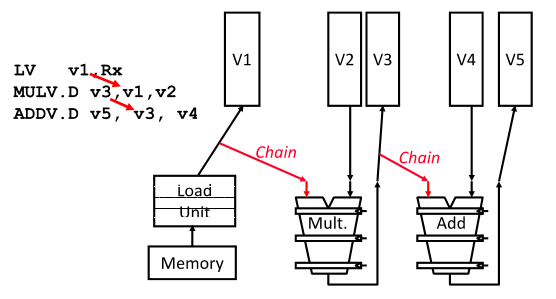
startup time을 중첩해서 사용하는 것이 Chaining 기법
Vector Length
Vector register 사이즈 만큼 잘라서 사용해야함
Strip Mining
Max Vector Length 보다 큰경우 자동적으로 나누어 코드를 generation 하는 것
나머지 먼저 처리하고 뒤에 Max Vector Length 만큼 쭉 처리함
1st loop do short piece(n mode MVL), rest VL
Vector Metrics
R: 백터엔진을 가동하면 어떤 응용을 주어도 상응하는 성능이 나올까? 가장 ideal 한 상태에서 얻을 수 있는 것은 무엇일까? 무한히 리소스가 많아 start-up 같은 제약도 무시될 수 있는 상황에서 얻는 가장 이상적인 성능
N(1/2): ideal 성능의 절반을 얻을 수 있는 vector 의 length
N(v): 파이프라인 start up latency가 존재하는데, 파이프라인을 가동해서 얻을 수 있는 효과는 start up latency 보다 많아야함(Scalar 보드로 수행할 때 보다 vector로 돌려 성능이 좋아지기 시작하는 minimum vector의 길이)
Vector Opt #1: Chaining
RAW 해저드 발생했을 때 v1에 어느정도 채워지면 다음번에 연산으로 주는 것이 Chaining
Vector Opt #2: Sparse Matrices
Sparse Matrices 는 non zero 만 모아서 vector 로 형성하는 동작이 gather(LVI) 명령어임
gather 후 수행결과를 다시 orginal 명령어에 저장하는 것을 scatter(SVI)
Vector Opt #3: Conditional Execution
Vector-mask control: element 별로 1bit이 bool 변수를 통해 조건 계산해 수행할지 안할지 저장