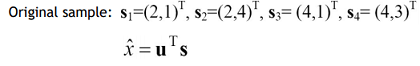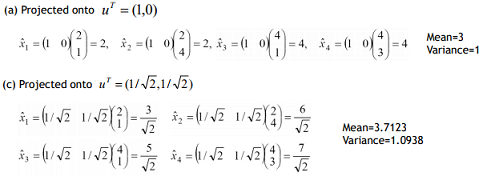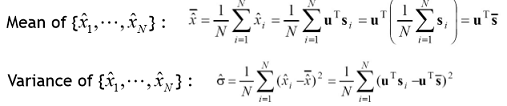Machine Learning 문제를 다루다 보면 high dimensional 데이터를 다뤄야 하는 일이 많이 발생
dimension 이 높게 되면 Curse of Dimensionality의 문제가 생김
Curse of Dimensionality 는 데이터의 dimension이 높다면 complexity에 영향을 주는 경우가 많으므로 알고리즘의 성능에 악영향을 끼치는 경우가 많음(Overfitting 도 존재)
따라서 dimension이 높다면 다양한 방식의 dimensionality reduction 기술을 적용해 데이터의 차원을 낮추는 작업을 하는데 대표적으로 PCA, LDA가 있으며 ICA, CCA 방법도 존재
Feature Extraction
차원이 높다는 것은 feature의 개수가 많다는 것을 의미
모든 feature가 전부 의미있는 feature는 아닐 수 있다는 것이 함정
의미있는 feature를 뽑아내는 과정을 feature extration이라고 함
dimensionality reduction 방법을 사용해 feature를 뽑아낼 수 있음
100개의 feature를 가지고 있을 때 가장 좋은 30개의 feautre만 뽑기 위해 30차원으로 dimensionality reduction을 함
PCA
PCA(Principal Componet Analysis)
dimension을 reduction 하는 것이 주목적
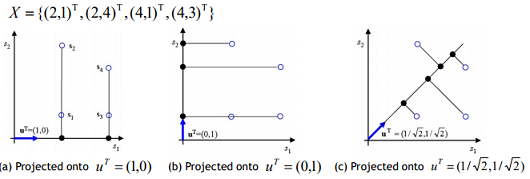
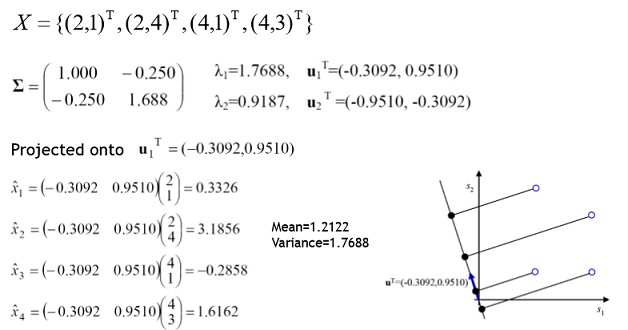
위의 그림은 2차원을 1차원으로 차원을 축소시킴
각각 U^T 백터로 Project 시키면 a는 x 값만 추출(2, 2, 4, 4 -> 값이 2개로 줌), b는 y 값(1, 4, 1, 3 -> 값이 3개로 줌)만 추출하는 로직임
c로 Project 시키면 모든 점 4개가 해당 백터에 표현됨
어떻게 Projection 시키는 것이 좋은 것일까?
원래 가지고 있는 data와의 error를 최소화 하는 것이 좋은 압축방법!
= sample들의 분산을 가장 크게하는 축(u)를 찾는 것
위의 그림에서 c처럼 Projection 후 4개의 점이 모두 표현 가능하여 가지고 있는 정보의 손실이 없음
가지고 있는 정보의 손실을 줄이려면 분산이 많이 퍼진 Projection이 좋은 것임
정보의 손실이 일어나 중복되면 Classification 할 때 구분하기 힘들어지기 때문임
PCA(2)
분산을 가장 크게하는 축(u)를 어떻게 찾을 것인가?
위에서 봤던 Sample에서 a축을 찾았을 때랑 c축을 찾았을 때 각각 평균분산 구해보면 c가 분산이 더 크므로 더 좋은 Projection 축임
PCA(3)
Projection한 Sample(N개)들을 X^^으로 표현하면 아래와 같은 수식으로 나타낼 수 있음
평균은 원래 Sample들의 평균을 내서 U^T에 Projection 한 결과와 같음
결국 위의 분산식의 값을 최대화하는 U를 찾는 것이 목적
Lagrange multiplier를 이용하여 찾음!
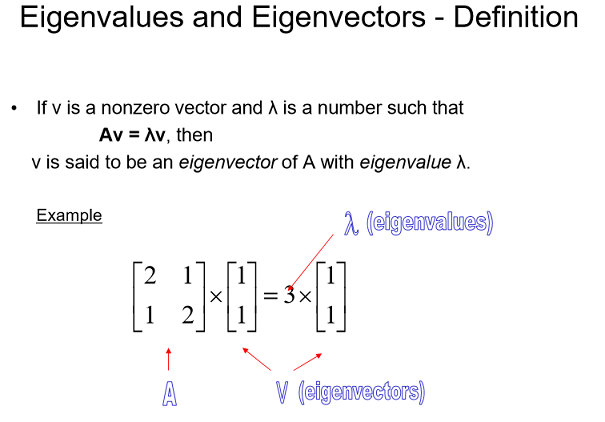
Lagrange multiplier?
간단히 말하면 Optimization Problem에서 maxf(x), minf(x)를 만드는 x를 찾는 것임
ex) f(x) = (x-2)^2 + 3 일 때 x가 2일 때 최소값 3을 가짐
여기에 만약 x에 조건이 있다면 5≤x≤6 이라면 x가 5일 때 최소값 12를 가지는 문제로 바뀜
조건이 있을 경우 더 복잡한데 부등호조건보다 일반적으로 등호조건이 더 쉬움
=0 조건일 때 Lagrange multiplier로 풀수 있음
Constraint가 있지만 없는 것 처럼 보임
L(x,lambda) - f(x) + lambda * g(x)
lambda = Lagrange multiplier
L(x, lambda) 를 각각 x, lambda에 대해 미분해서 0을 만드는 x, lambda를 구하면 원래 구하려는 값과 동일함
다시 원래로 돌아와서 분산식의 값을 최대화하는 U를 찾기위해 lagrange multiplier를 이용하고 이를 위해 U^T*U = 1 이라는 조건을 추가함
U^T*U = 1 이라는 조건은 Projection 시킬 U를 찾는데 길이가 1인 백터 즉 normalized 된 백터를 쓰겠다는 것임
L(u, lambda) 에서 lambda에 대해 미분하면 U^T*u-1 =0 이므로 추가된 조건을 만족함
이제 u에 대해 미분한 것이 0인 것만 찾으면 됨
미분해보면 결국 U는 Covariance matrix ∑ 의 eigenvector임
= Sample들의 covariance matrix의 eigenvector를 구하면됨
아까 Sample들의 covariance matrix를 구하고 eigenvalue가 가장 큰 것을 선정해 Projected 시켜보면 분산이 1.7688 로 제일 큰 값을 찾을 수 있었음
PCA Algorithms
eigenvalues중 큰 것 d개만 뽑아서 (n*d) 의 matrix U를 만듬
Recognizing images using PCA
이미지를 1차원의 vector로 표현하고 sample 들의 평균을 구함
Sample에서 Sample들의 평균을 빼서 이미지를 centered 시킴
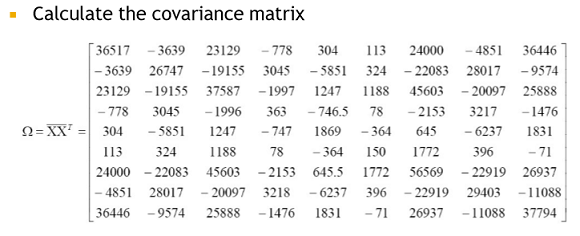
centered 된 matrix의 Covariance matrix를 구함
centered 된 matrix * (centered 된 matrix)^T로 표현 가능
cf) Cov(x,y) = E((x-m)(Y-m)) = E(xy) - E(x)E(y)
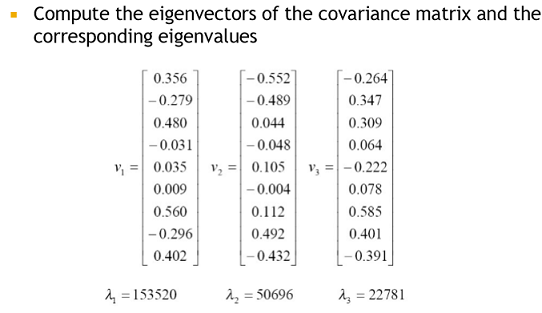
Covatriance matrix의 eigenvector와 eigenvalue를 구함
cf)
det(A-lambda*I) = 0 인 것을 풀면됨
lambda가 0아 아니므로 위의 A-lambda*I가 역행렬이 존재하면 안됨(존재하면 lambda가 0이 될 수 있음)
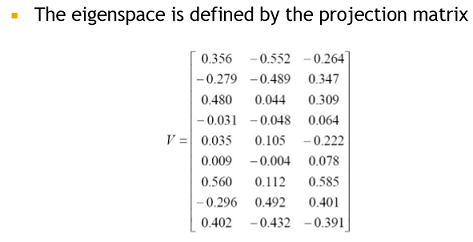
V가 결국 아래 행렬처럼 나옴
V^T는 (3x9) 행렬이므로 V^T * Sample1 하면 (3x9) * (9x1) 이 됨으로 (3x1)로 차원이 줄어듬
Test
y의 값이 다음과 같이나오고 이는 X^^2와 가장 값이 유사함
유클리드 구해서 가장 가까운 것을 구하면됨