PCA를 이용해서 얼굴인식하는 과정

Image Representation

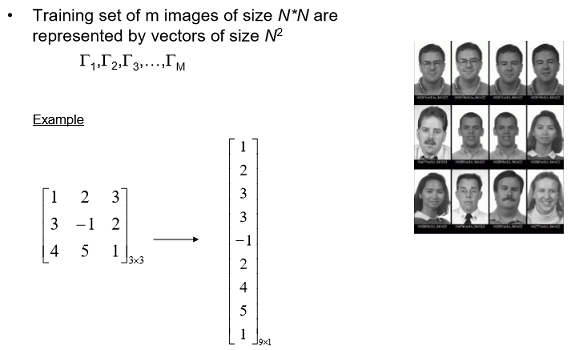
이미지 matrix를 백터화 시킴

Average Image and Difference Images

백터화된 이미지들의 평균을 각각의 image에서 빼줌

Covariance Matrix를 구함

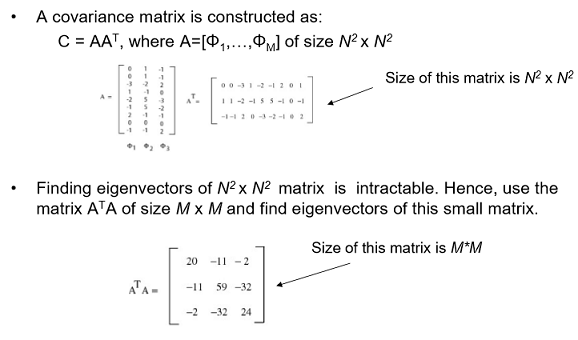
여기서 AA^T의 Covariance Matrix를 구해야하지만 N^2*N^2 으로 차원이 너무커 A^TA의 Covariance Matrix를 구함

이 둘 사이에 eigenvalue는 같고 eigenvector만 다른 특성을 이용

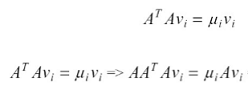
위의 식에서 Avi를 vi’으로 치환해보면 뮤i 가 같음(뮤i = eigenvalue)

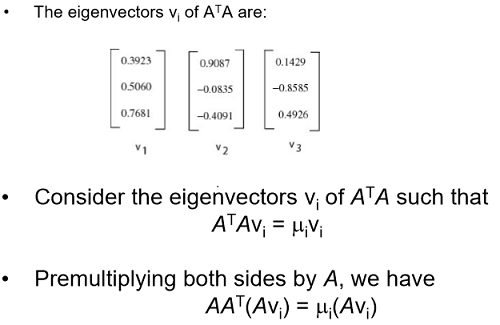
Face Space

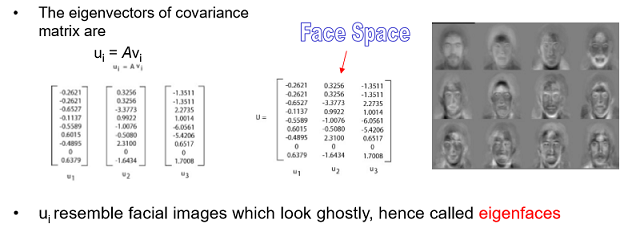
A^TA를 통해 구한 eigenvector 중 k 개를 뽑은 것을 U = Face Space라 부름

Projection into Face Space

위에서 구한 Face Space를 통해 차원을 축소하고 Sample과의 거리 중 가장 가까운 것으로 Classification 하면됨

PCA using SVD

SVD - Singular Value Decomposition

행렬 Decomposition 특성을가지고 PCA를 수행할 수 있음

S^2 이 eigen value의 역할을 하는 것이 핵심

Limitations of PCA

전체데이터의 분산만 고려되기 때문에 Classification 을 하기에는 부족함

분산이 크다고 feature들을 구별하기 위한 좋은 feature 라고 보장할 수가 없음

=> LDA(Linear Discriminant Analysis = Fisher Discriminat Analysis(FDA)) 가 나온 배경