Ranked Retrieval
Ranked Retrieval
전문가 - 그들이 원하는 collection이 무엇인지 정확하게 이해하고 있음
검색결과가 1000개가 나와도 쉽게 인지하기 쉬움
대부분 주요 유저 - Boolean queries를 쓰는데 유능하지 않음
대부분 유저들이 1000개씩이나 나오는 결과를 원하지 않음
이것이 web search 의 현실임
Problem With Boolean Search:Feast Or Famine
Boolean queries는 너무 많은 결과를 내거나 너무 적은 결과를 냄
ex) “standard user dlink 650” -> 200,000 hits
ex) “standard user dlink 650 no card found” -> 0 hits
And는 결과의 수를 줄이고, Or은 결과의 수를 많이 늘림
Ranked Retrieval Model
documents의 집합말고, Ranked Retrieval에서는 query에 만족하는 (top)documents의 순서를 return 함
Free text queries: query language의 연산과 표현대신 유저는 사람이 쓰는 하나 이상의 단어로 질의할 수 있음
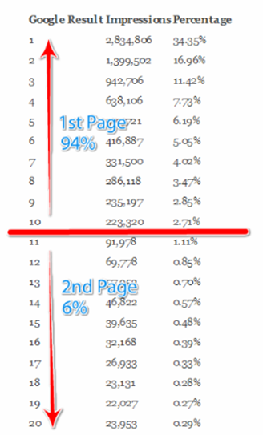
Feast Or Famine : Not A Problem In Ranked Retrieval
Feast Or Famine 문제가 랭킹 모델에서는 문제가 되지 않음
큰 result set이 문제가 되지 않는 다는 뜻!
top k 만큼의 result만 보여주면 되기 때문임
Scoring documents
Scoring As The Basis Of Ranked Retrieval
document의 rank 순서를 어떻게 매길 것인가?
0~1 사이 값을 각각의 document에 할당하고, 이 스코어는 document와 query 가 얼마나 잘 일치하는 지를 측정한 값임
query term이 document에 전혀 나오지 않았다면 0
query term이 자주 나올 수록 score는 높아져야 함
Take 1: Jaccard Coefficient
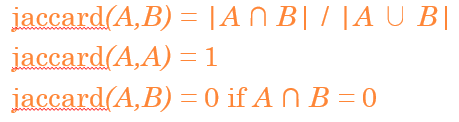
Quiz
What is the query-document match score that the Jaccard coefficient computes for each of the two documents below?
Query : ides of marches
Document 1: caesar died in march
Document 2: the long march
J(q, d1) = 1/6, J(q, d2) = 1/5
Issues With Jaccard For Scoring
Jaccard Coefficient는 term frequence를 고려하지 않음
길이를 정규화 시켜 더 정교화된 방법이 필요함(합집합에 루트)
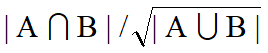
Term Frequency
Term-document Count Matrices
이전에는 document에 term이 있는지 없는지 0, 1로만 나타냄
해당 document에 term이 몇번 나왔는지 까지 고려하는 행렬
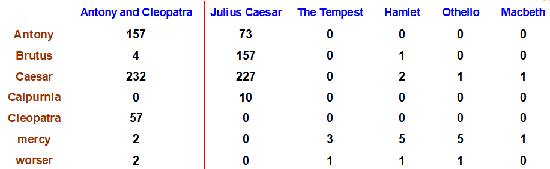
행렬의 값은 단어의 frequency를 나타냄
Bag Of Words Model
Vector의 표현은 document 안에서 단어의 순서를 잃어버림
John is quicker than Mary and Mary is quicker than John은 같은 백터를 가질 것임
Bag of Words
document 를 categorize 하기위함이 목표
다른 두개의 bags of words(corpus)를 분류하고 분석하기 위한 아이디어
예를 들어 spam filtering 같은 곳에 사용됨
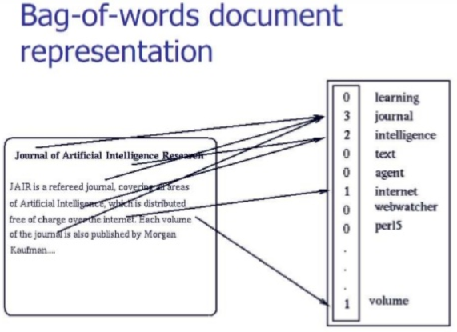
위의 그림과 같이 단어와 frequency를 백터화
Term Frequency TF
tf(t,d) - term t가 document d에 t번 발생하는 수를 뜻함
우리는 tf를 query와 document를 match 하는 score에 사용하고 싶은 것임
그러나 Raw term frequency는 만일 document에서 10번 발생하는 term과 1번 발생하는 term이 있을 때 10번 발생하는 것이 더 relevant 할 것임
그러나 그 값이 10배는 아님!(연관도가 term frequency와 비례해서 증가하지는 않음)
frequency 는 IR에서 count를 의미
Log-Frequency Weighting
tf값에 log를 취함
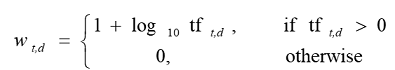
0->0, 1->1, 2->1.3 등등 이런 식으로 됨
query와 document에 모두 있는 terms t 를 log 취한 값으로 부터 1을 더해 모두 sum함
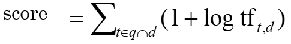
만일 query terms가 document에 나오지 않는다면 score는 0임
Document Frequency
Rare terms이 frequent terms 보다 더 중요할 수 있음(Recall stop words)
query의 term중 collection에서 드문 단어(ex, arachnocentric)를 고려하자
arachnocentric와 같이 collection에서 드문 단어를 포함하고 있는 document는 query에서 arachnocentric로 검색할 때 드물지만 매우 연관이 있을 것임
(즉, rare term에 높은 weight를 주고 싶음)
idf weight
df(t)는 documents에 t를 포함하는 수를 의미( ≤ 전체 document 수 N) 이 df(t)를 inverse 시켜 rare한 것이 높은 점수를 가지도록함
따라서 idf(inverse document frequency) 를 아래와 같이 정의함
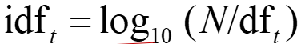
log를 취한 것은 idf 의 영향력을 약화시키기 위해 사용함(log를 취하는 것이 영향력이 없다고 증명됨)
Effect Of Idf On Ranking
idf는 one term queries(iphone)의 ranking에는 영향을 미치지 않음
idf는 전체문서수/그단어가 포함된 문서수에 log를 취한 값으로 볼 수 있음
query와 전체 corpus에 의존적이며 document에는 의존적이지 않아 모든 document에 대해 constant로 볼 수 있고 TF-IDF 점수는 모든 상수에 대해 동일하게 확대/축소되므로 랭킹에 영향을 미치지 않음
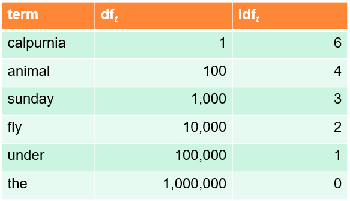
위의 표를 보면 term하나에 대해 idf 는 고정되어 있음
tf-idf 로 보면 idf의 값은 상수 값이 됨
Collection Statistics
Collection vs Document frequency
Collection의 frequency는 multiple occurrences 까지 모두 새고 Document frequency는 unique한 것들만 포함 시킴

collection frequency의 값은 insurance 와 try가 거의 비슷
insurance 가 2~3번 정도 더 많이 사용된 것임(잘고려해서 사용해야함)
Weighting Schemes
tf-idf Weighting
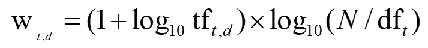
tf값과 idf값을 곱한 것을 weighting으로 이용하며 ir 분야에서 가장 잘 알려짐
document에서 많이 나올 수록, rare한 term일 수록 값이 증가
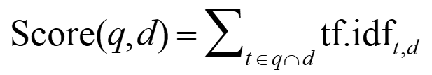
Matrix를 Binary->Count->Weight로 변경됨
Vector Space Scoring
Documents As Vectors
| V | 차원의 vector space가 있다고 할 때 space에서 term들이 축임 |
Document는 pointer이거나 vector임
Web Search Engine에 이것을 적용할 때 고차원이 되버림 -> 그러나 very sparse 한 vector임(대부분 0)
Queries As Vectors
key idea 1: queries 자체를 vector로 표현함
key idea 2: query와의 유사도에 따라 document를 랭킹매기는 방법 존재
유사도는 유사성 vector이며 distance의 inverse 값임(거리가 멀수록 유사성은 떨어짐)
Formalizing Vector Space Proximity
First cut : 두 points간의 차이
Euclidean distance?
distance is a bad idea
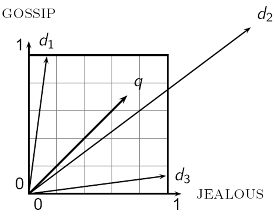
q와 d2가 가장 멈
d2rk GOSSIP과 JEALOUS 의 중간인 d2가 원래 가장 유사한 것이지만 거리상에서는 가장멈
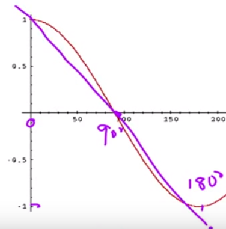
angle을 사용하자
From Angle To Cosines
query와 document 사이에 angle 이 작은 순서대로 Ranking을 매기는 것 = cosine(query, document) 가 증가하는 순서대로 Ranking을 매기는 것
0~180도에서 cosine함수는 감소하는 함수
cosine을 어떻게 계산할 것인지?
Length Normalization
vector는 자신의 길이로 나눠 Normalize할 수 있음
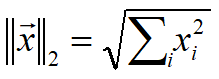
위의 식을 L2 norm이라 부름
L2 norm으로 나누면 vector는 크기가 1인 unit vector가 됨
cosine(query, document)
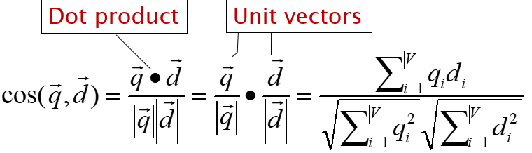
normalized 시키면 아래가 1이 된 unit vector간의 dot product만 하면됨
Cosine Similarity Illustrated
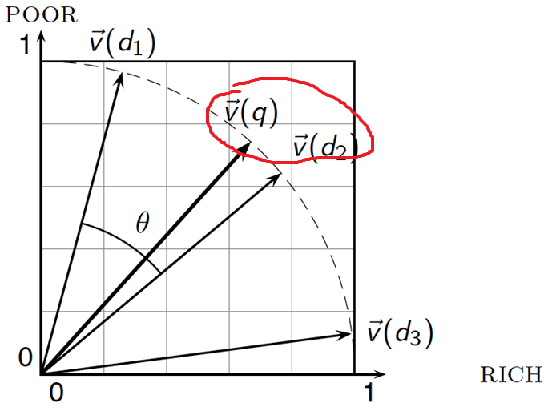
angle이 작은 d2가 q에 가장 유사함
Cosine Similarity Amongst 3 Documents
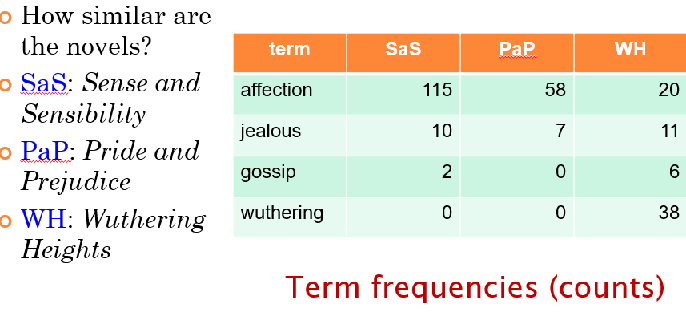
Term frequencies를 가지고 Log를 취함(idf는 계산 편의상 뺌)
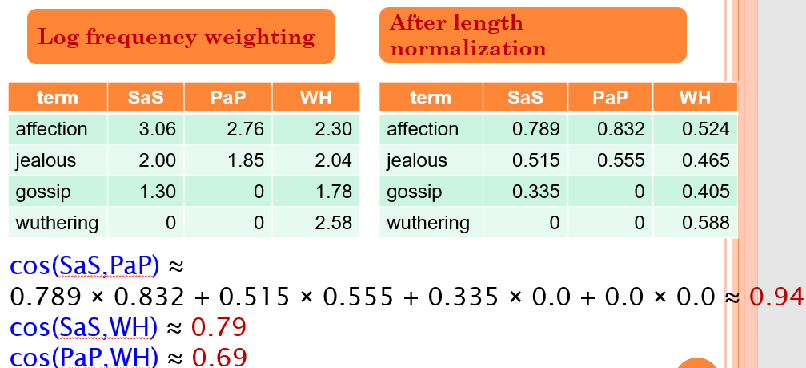
이후 length normalization하고 cosine similarity를 구하면 SaS와 PaP가 제일 유사함
TF-IDF Weighting has Many Variants
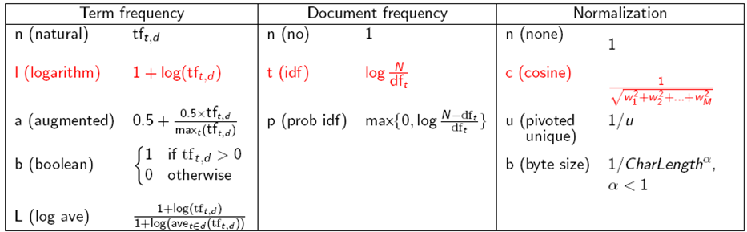
여러가지 조합으로 이용
Weighting May Differ In Queries vs Documents
Document는 logarithmic tf와 no idf, cosine normalization 이용(lnc)
Query는 logarithmic tf, idf, no normalization 이용(ltc)
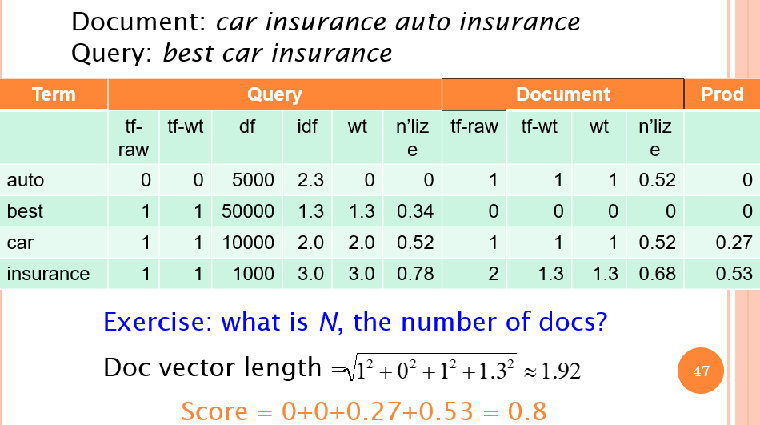
Summary
query를 tf-idf vector로 weighted
document를 tf-idf vector로 weighted
query vector와 document vector 간의 cosine similarity score 계산
score를 기반으로 document를 Rank 시킴
유저에게 top K 리턴