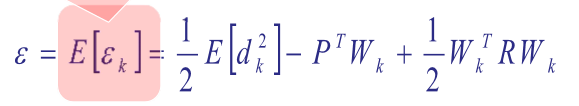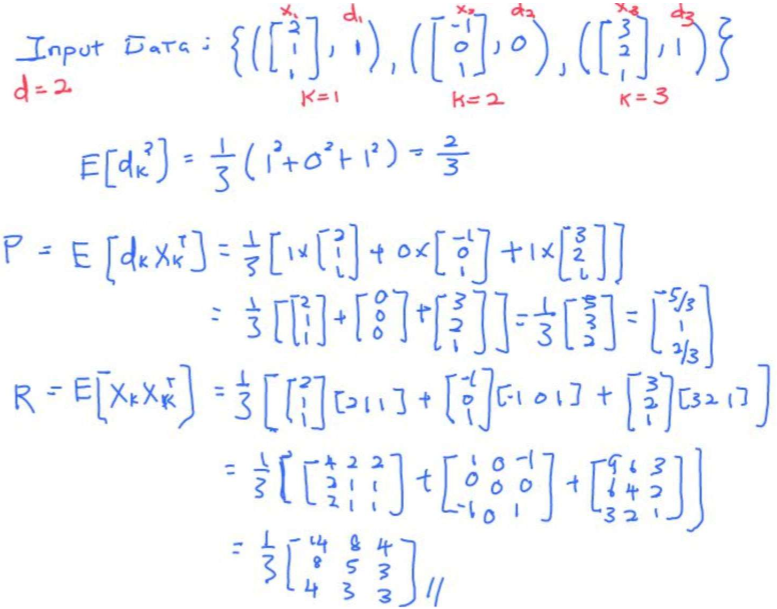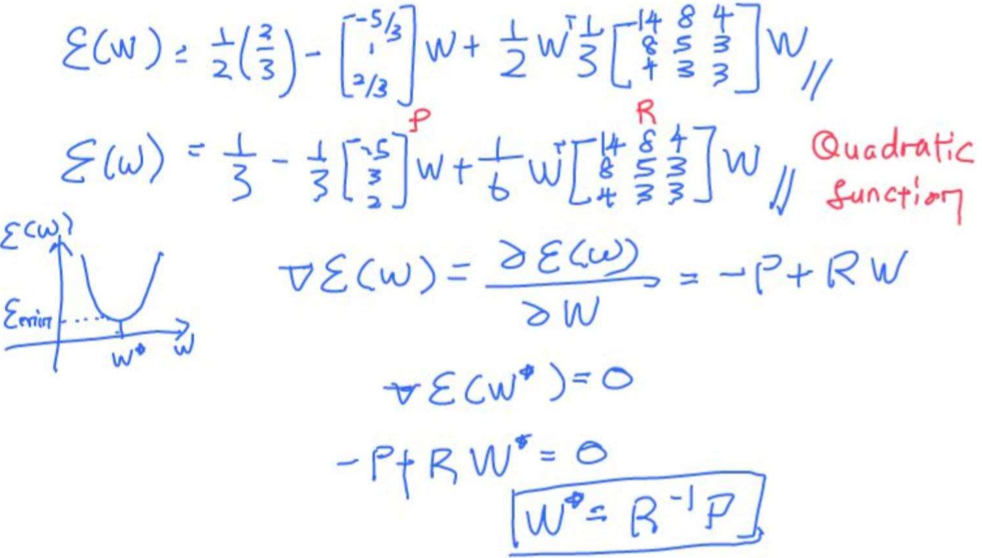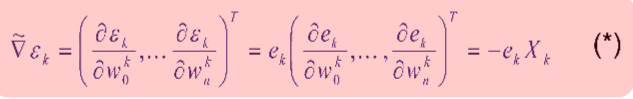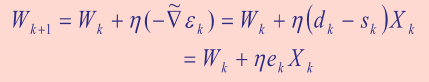Close Form Solution

straightforward differentiation에 의한 gradient 계산

미분해서 0이 되는 지점을 찾음 (W = R^-1 * P => Weiner solution)

Summary

매우 정교하고 한번에 solution을 결정할 수 있는 장점이 있음

단, R은 matrix 며 inverse 가 가능해야함(singular matrix 같은 경우 inverse 구하지 못함)

inverse 가 가능하더라도 x의 element 가 많으면 Inverse 를 계산하는 비용이 매우 비쌈

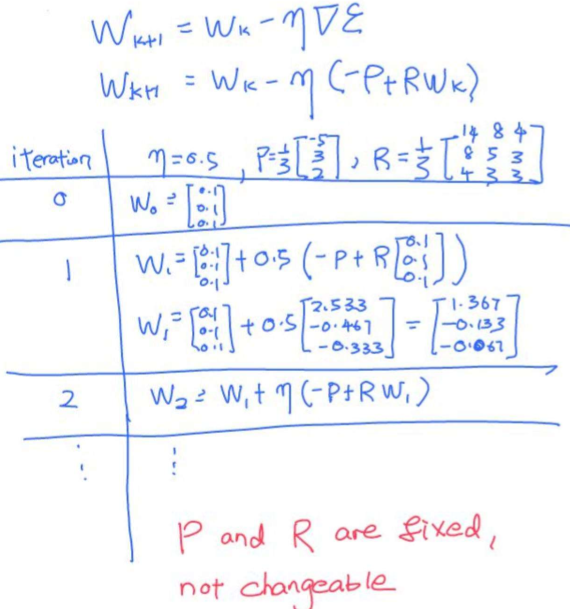
Example

Batch Gradient Descent(BGD)

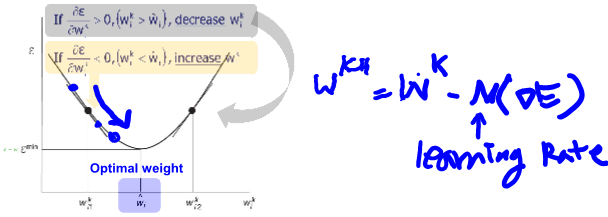
처음에는 random initial vector (미분 값에 따라 방향이 결정됨)

계속 수행해서 결국엔 최소화 시키는 error 값에 도달하는 것이 목표

learing rate 가 stepsize를 결정하며 이 값이 너무 작으면 traing 하는데 오랜 시간이 걸릴 수 있고 너무 크면 oscillates(왔다갔다 진동) 하거나 diverge(벗어남) 할 수 있음

Batch - individual data를 combine vector 형식으로 만듬

gradient error 가 -P + R*W(k) 가 됨(Exact gradient error information -> 순간 기울기의 개념)

따라서 R의 inversion이 필요하지 않음

Example

Problems of BGD

Exact gradient information은 data set 전체에 대해 미리 지정되어 있어야 R, P를 정확히 계산하고 iteration을 돌 수 있음

Problem 1: data set 이 random stream 한 패턴일 경우 R과 P를 계산할 수 없음

Problem 2: P와 R을 높은 차원에세 계산하기에 비용이 비쌈

Stochastic Gradient Descent(SGD)

data 전체를 보는 것이 아니라 데이터 하나하나 에러를 통해 계산

SGD covergent in the mean if the average of weight vector W(k), approaches the optimal solution W(opt) as the number of iterations k, approaches infinity: E[W(k)] -> W(opt) as k -> ∞

X(k)를 각각의 data 를 뜻하고 e(k)도 각각 data에 대한 error 임

weight는 아래 공식에 의해 update 됨

epoach자체가 전체 데이터에 대해 한번 돈 것이 하나의 epoch 임

BGD vs SGD

BGD - Use global gradient info (Heavier Computation Effort)

SGD - Use local gradient info (Usually take more iterations to reash solution)

Mini-Batch Gradient Descent

Batch 와 Stochastic modes의 중간정도 개념

Batch size 만 큼 SGD 수행하여 각각 구한 e의 평균을 통해 W를 update 시킴