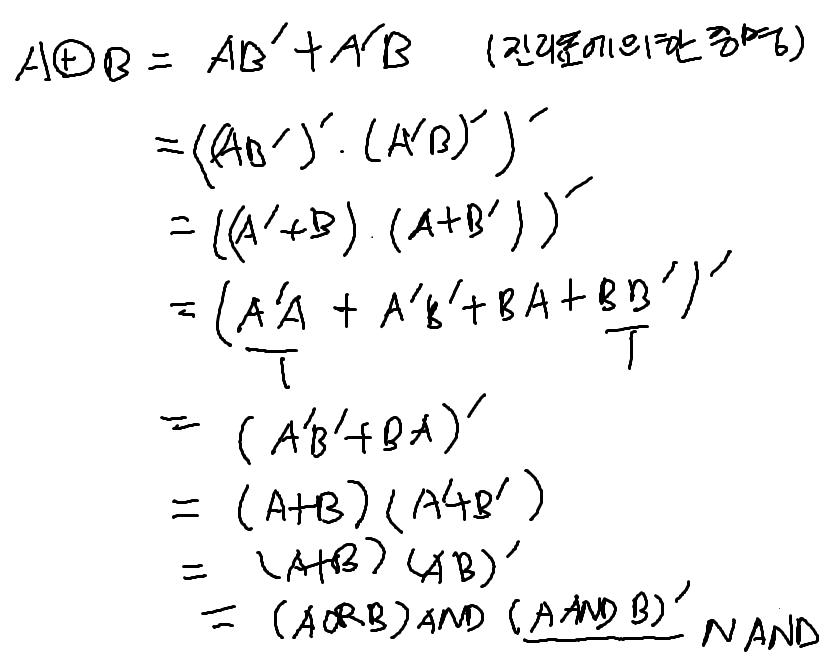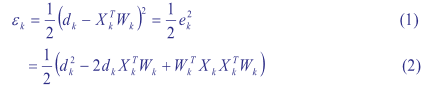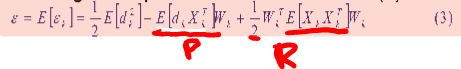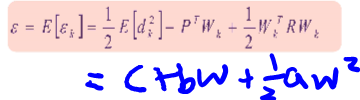Linearly non-separable data

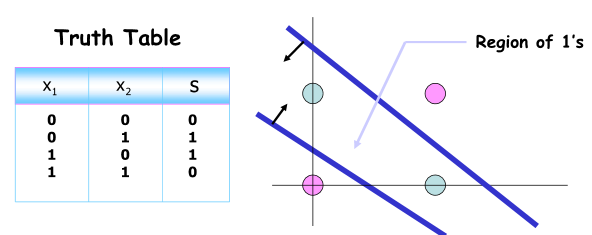
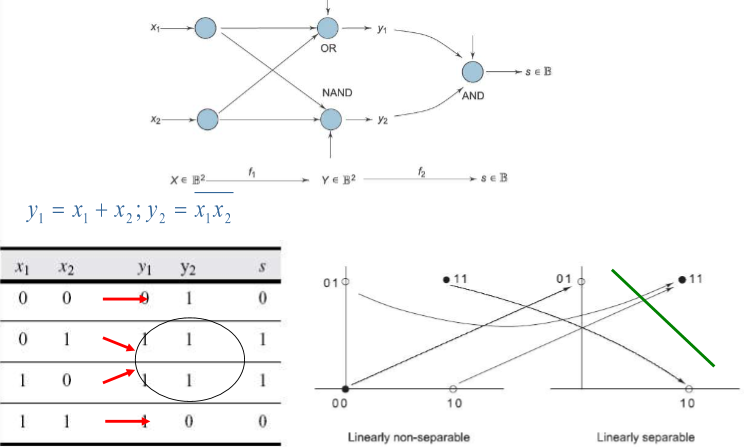
XOR is Not Linearly Separable

OR, AND, NAND는 하나의 perceptron으로 classification 문제를 풀 수 있었지만 XOR은 하나로 불가능함

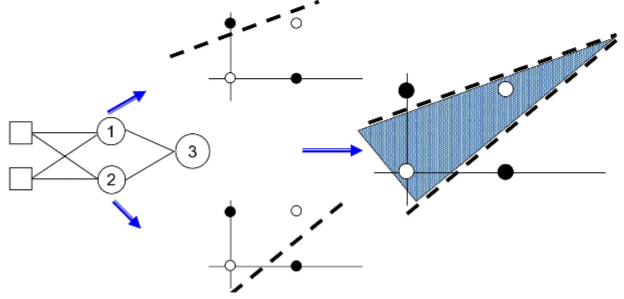
Three Perceptrons Are Required

2개의 뉴런이 각각 두 개의 hyperplanes를 만들고 또 다른 뉴런이 앞의 두 개의 hyperplane을 하나로 연결시킴

XOR Decomposition

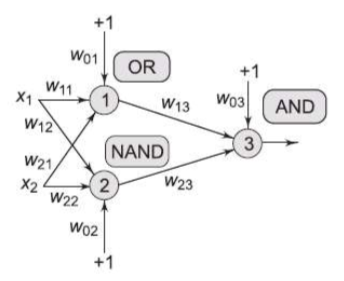
Network of Perceptrons to solve XOR

Interpretation

X 공간에서 새로운 Y 공간으로 가는 효과

Y 공간에서 새로운 s 라는 공간으로 mapping 됨

s 공간에서는 Linearly separable로 classification 할 수 있음

Supervised Learning

Gradient Descent Algorithms

Close form solution, BGD, SGD, Mini-batch Gradient Descent

Perceptron without Step Activation Function

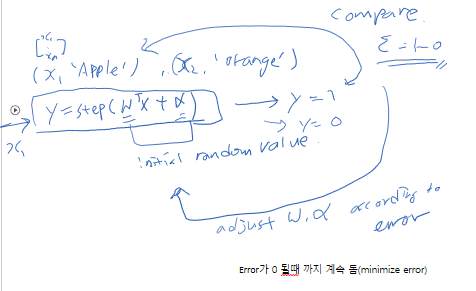
ADALINE - perceptron without step function

Training set 이 T = {Xk(input), dk(label)} 의 형태라고 하자 Xk∈R^n+1, dk∈R(label)

output을 vary smmothly or continuously 하기 위해 linear activation function 을 지정

s(k) = y(k) = X(k)^T * W(k)

activation function 에 y(k)를 input 으로 해서 나온 output s(k)를 가지고 Classification 수행

Classification : If s(k) > 0, class 1 and otherwise

Training data error: (x(1), d(1)) -> e(1) = d(1) - (X(1)^T * W(1))

Mean Squared Error(MSE)

e(k) = d(k) - s(k) = d(k) - (X(k)^T * W(k))

error에 양수 음수 모두 있는 경우 양수로 만들기 위해 squared error 로 변경함

traing data 각각에 대해 error 가 존재하고 이를 평균을 취하는 것이 mean-squared error(MSE)

k = 1, 2, 3 … Q(training data num)

E[∈(k)] = 1/Q (∑(∈(k)))

MSE 를 supervised learning 에서 loss function이라 부름

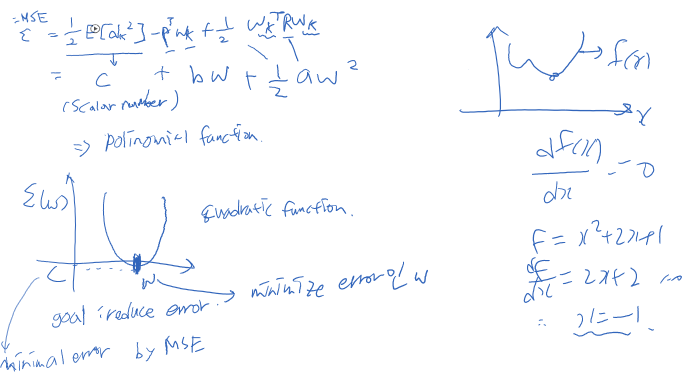
위와 같이 polynomial function으로 나타낼 수 있으며 이차함수형태임 -> quadratic function

Our Problem

mean-square error 를 최소화 시키는 optimal weight vector(W(k)) 를 찾는 것!