Ubuntu 20,04 기반 ROS2 Foxy 로 TurtleBot3 Waffle Pi 구동 과정 정리
SLAM
TutleBot3 Waffle Pi 는 360 Laser Distance Sensor(LDS) - Lidar 즉, 360도 2차원 레이저 스캐너 HW와 ROS2 Dashing 에서는 Cartographer 를 default SLAM 알고리즘으로 사용
참고 문서
- https://www.youtube.com/watch?v=_i8PaekcguA
- https://adioshun.gitbooks.io/deep-slam/content/SLAM-kr-Tutorial/chapter-2.html
- http://jinyongjeong.github.io/tag/SLAM/
Lidar 센서란?
- Radar는 전자기파를 내보내 물체를 감지하고, 물체에 반사된 전파를 분석해 거리나 속도 등을 측정하는 부품(저렴하지만 물체의 형태 인식 불가)
- Lidar는 레이저를 내보내 물체를 감지하고, 반사된 빛을 분석해 지도로 구현하는 부품
- Lidar는 레이저가 반사되어 돌아오는 시간 및 강도를 측정하고 이를 통해 방향, 속도, 온도, 물질의 농도 등의 특성을 파악 할 수 있음
- Lidar 의 비싼 가격으로 개발 초기 360도 회전식 스캔 장비에서 고정형 라이더 센서 개발로 가격을 내리고 있음(고정형 라이다 센서를 여러군데 부착)
- 카메라는 빛을 흡수하여 장면을 담기 때문에 빛의 영향을 받지만 라이다는 빛의 영향을 받지 않음(카메라와 비교해서 상당히 많은 환경에서 안정적으로 장애물을 인지하고 예측 가능)
- 그러나 최근 카메라 기술이 좋아져 라이다를 대체하려고 하며, 테슬라 머스크는 레이더, 초음파센서(보통 차량 후방 주차감지에 쓰임), 카메라만으로 자율주행 구현함
Lidar vs Radar 센서 비교
- 거리측면 : 라이다는 근거리 물체를 감지하기 어렵지만 레이더는 1m도 안 되는 거리의 물체부터 200m 이상 까지 감지되지만 시스템 유형(단거리, 중거리 등)에 따라 달라짐
- 공간 분해능 : 라이다는 백엔드 프로세싱 없이 물체들의 특징을 한 장면으로 3D 묘사 가능, 레이더의 파장은 거리가 늘어날수록 작은 특징들을 분석하는데 어려움
- 날씨조건 : 레이더는 비, 안개, 눈에 강하다, 라이더는 비, 안개, 눈 날씨 조건에서 성능 하락
- 라이다와 카메라는 둘 다 주변 광 조건 영향을 받기 쉽지만 야간의 경우 라이다가 높은 성능을 보임, 레이더는 다른 센서들의 간섭에 강함
Lidar SLAM
- Lidar sensor 입력을 기반으로 localization 과 Mapping 수행
- LOAM 이 대표적인 SOTA알고리즘 중 하나임
- https://www.ri.cmu.edu/pub_files/2014/7/Ji_LidarMapping_RSS2014_v8.pdf
Visual SLAM 카메라
- 단안카메라 : 카메라 하나만 사용(거리정보를 상실하며, 진정한 스케일 확인 불가)
- 양안카메라 : 두 카메라의 거리 정보를 기반으로 깊이를 추정(실내외 모두 사용 가능)
- 깊이카메라 : Time of Flight(TOF) 또는 적외선 구조광 방식으로 측정해 깊이 값을 예측(좁은 범위, 높은 노이즈, 작은 시야, 햇빛에 쉽게 노출, 투과 물질 측정 불가)
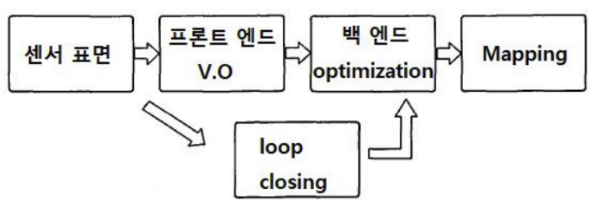
고전적인 시각적 SLAM 프레임 워크
- 센서 정보를 읽는다
- 시각적 SLAM에서는 주로 카메라 이미지 정보의 읽기, 전처리 단게
- Visual Odometry(Front End)
- 시간 또는 인접한 이미지 사이의 카메라 동작과 로컬 맵의 모양을 추정
- Backend Optimization
- loop closure 에 대한 정보는 물론 시각적인 주행 거리계로 측정한 카메라 포즈를 받아들이고 일관된 궤도와 맵을 얻을 수 있도록 최적화
- Loop Closure
- 로봇이 과거에 도할했던 위치에 도달했는지 확인하는 역할을 수행
- Loop Closure가 감지되면 처리를 위해 백엔드에 정보를 제공
- 맵핑
- 추정 된 궤도를 기반으로 현재 위치에 해당하는 지도를 만듬
- Visual Odometry

- 카메라가 어느 방향으로 얼만큼 이동했는지는 vo로 계산 가능
- vo는 에러가 누적됨(=Drift Problem)
- 해결법 #1: Loop Closure Detection(이전 방문 탐지)
- 해결법 #2: Backend Optimization(Loop Closure를 통해 전체 트랙 모양 수정)
- 벡엔드에 최적화 할 데이터와 데이터의 초기 값을 제공(데이터 자체를 다루는 역할)
- Backend Optimization
- SLAM의 노이즈를 처리하는 문제를 수행
- 잡음이 많은 데이터로 부터 전체 시스템의 상태를 추정하는 방법
- 상태 추정치가 얼마나 불확실한 지 계산(사후확률추정, MAP-Maximum a Prior)
- Loop Closure Detection
- 시간에 따른 위치 추정 문제를 해결하는 것을 목적
- 기본적으로 이미지 데이터의 유사도 계산(동일한 장소 이미지)
- 루프백을 감지하면 Backend에서 A와 B는 같은 지점임을 알려주고 이 정보를 기반해 궤도 및 맵을 조정
- 위의 방식으로 누적 오류를 제거하고 전역적으로 일관된 맵을 얻을 수 있음
- 맵핑
- 맵을 빌드하는 과정
SLAM 문제의 수학적 표현
- 모션 모델 (motion model)
- 로봇의 위치가 어떻게 변하는지를 표현
- 로봇이 $x_{k-1}$ 위치에서 컨트롤 입력 $u_k$ 를 받았을 때 새로운 로봇의 위치 $x_k$
- 로봇의 위치를 x라고 하면 x가 어떻게 변하는지 고려
- $ x_k = f(x_{k-1}, u_k, w_k) $
- $ u_k $: 모션 센서 입력 또는 컨트롤 입력
- $ f() $ : 모션모델을 나타내는 함수(계산 문제마다 달라짐)
- $ w_k $: 모션 모델에 대한 노이즈(실제 세계는 노이즈로 가득함)
- 관찰 모델 (sensor model)
- 랜드마크(환경)가 로봇에서 어떻게 관찰되는지를 표현
- 로봇이 $x_k$ 위치에서 어떤 랜드 마크 점 $y_j$를 볼 때 관측 데이터 $ z_{k,j}$가 생성된다는 것
- $ z_{k,j} = h(y_j, x_k, u_{k,j})$
- $ z_{k,j} $: 관찰값
- $ h() $ : 센서모델을 나타내는 함수
- $ u_{k,j} $: 센서모델에 대한 노이즈
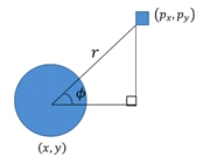
- 2차원 레이저 센서에서 2D 지표를 관찰할 때 지표와 로봇의 거리 r 과 각도 Φ의 두 가지 양을 측정 가능
- 랜드파크 $ y = [p_x, p_y]^T $ 로 기록하고 관측 자료는 $ z = [r, Φ]^T $ 이므로 관찰 방정식은 아래와 같음
- $\begin{bmatrix} \frac{r}{Φ} \end{bmatrix} = \begin{bmatrix} \frac{\sqrt {(p_x - x)^2 + (p_y - y)^2}}{arctan \begin{pmatrix} \frac{p_y - y}{p_x -x}\end{pmatrix}} \end{bmatrix} + u_{k,j}$
- SLAM의 상태 추정 문제로 모델링
- $ x_k = f(x_{k-1}, u_k, w_k) $
- $ z_{k,j} = h(y_j, x_k, u_{k,j}) $
- 상태 추정 문제에 대한 해답은 두 방정식의 특정 형태와 노이즈가 어떤 분포를 갖는가와 관련이 있음
- 예를 들어 모션 및 관찰 방정식을 선형으로 분류하고 잡음이 가우스 분포를 따르고 선형/비선형 및 가우시안/비 가우시안 시스템으로 나눌 여부를 고려하게 됨
- 이 중에서 Linear Gaussian 시스템은 가장 간단하며 Kalman Filter 를 사용하여 최적의 추정치를 얻을 수 있음
- 복잡한 non-liner non-Gaussian 에서는 확장 된 칼만 필터(EKF)와 비선형 최적화 방법을 사용하여 해결
- 과거 / 현재 기법
- 현실은 비선형 문제가 주를 이룸
- 21세기 초까지 EKF(Extended Kalman Filter) 를 이용
- 그러나 EKF SLAM 은 선형화 과정에서의 오차의 단점이 존재
- 이를 극복하기 위해 파티클필터, 비선형 최적화 방법을 사용하기 시작
- 현재 Graph 기반의 SLAM 방법이 주류를 이루는데 이유는 Large Scale 에 적합하기 때문임(Computing Power 도 적합)