Generative vs Discriminant Approach
Generative - 각각의 클래스에 속하는 데이터들의 확률분포를 측정한 것
| P(W1 | X), P(W2 | X) - X가 주어졌을 때 W1 클래스에 속할 확률과 W2 클래스에 속할 확률을 구하여 큰 확률로 분류하는 것 |
Discriminant - Dicision Boundary 를 직접 구하는 것(ex. SVM)
Generative Approach(two categories)
| P(W1 | X) = g1(x)로 보고 P(W2 | X) = g2(x)로 봤을 때 아래와 같이 하나의 함수로 나타낼 수 있음 |
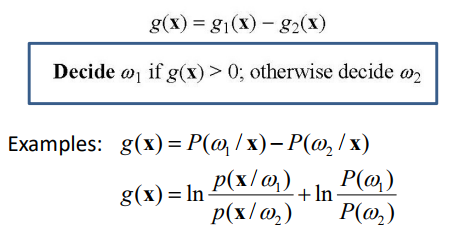
g(x) = 0 일 때 x는 decision boundary에 위치하며 W1, W2 둘다 될 수 있음
Person Authentication
Baye’s 이론에서 지문이나 무언가 등록이 되어있을 때 인증하고 안하고를 분류한다고 해보자
Authentication - Yes or No(등록된 사람과 같은지 판단)
Recognition - 여러명이 있을때 그중 무엇이냐로 인식하는 것
| P(W1 | X) = ( P(X | W1) * P(W1) ) / P(x) |
| P(W2 | X) = ( P(X | W2) * P(W2) ) / P(x) |
확률분포를 그림으로 나타내면

A 부분이 Authentic
I 부분이 Impostor
ROC Curve

threshold가 커질 수록 Reject를 많이하고 작을 수록 Accept를 많이 하는 것임
그래프에서 Y축이 Error rate이고 보통 Equal Error Rate(EER)을 가지고 시스템의 성능을 많이 이야기함
-> 만나는 점이 낮아질 수록 Error rate가 낮다는 뜻이고 이는 좋은 시스템을 의미
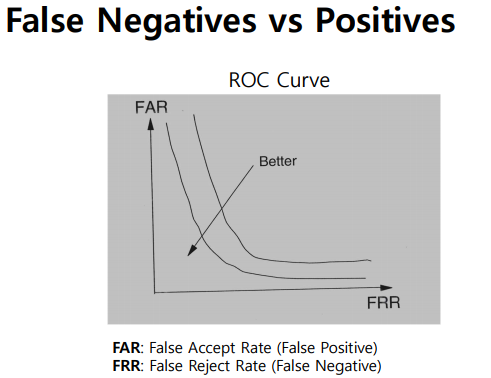
서로 반비례관계에 있음
Discriminant Approach(two categories)
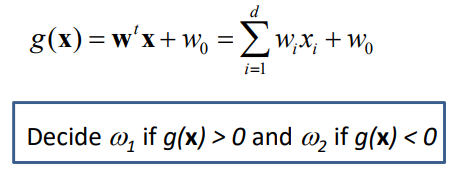
g(x) = 0 인 부분인 decision boundary 임
이 dicision boundary(hyperplane)가 linear 하다 -> linear discriminant
training 데이터를 사용하여 가장 best한 decision boundary를 찾으려면?
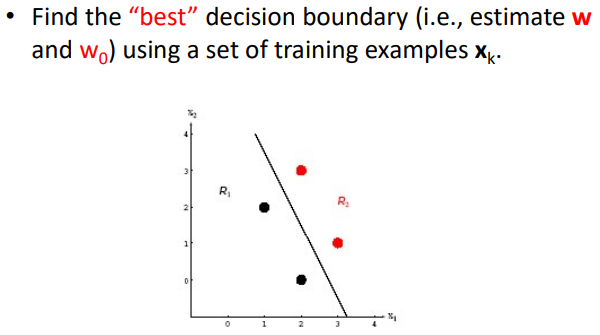
실제 분류한 class와 예측한 class 의 차이가 적도록하는 값을 가진 W를 찾으면됨
이 차이를 error function을 정의하고 이 함수의 값을 최소로 하는 값을 찾는 것이 학습!

Geometric Interpretation of g(X)
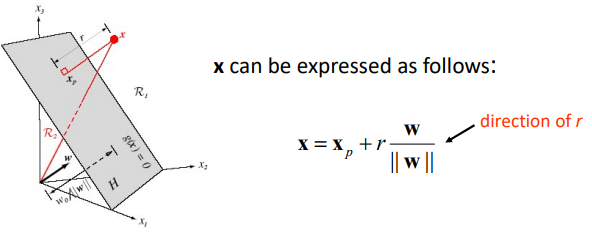
x 점은 xp에서 거리가 r만큼 떨어진 자리에 위치함
| W/ | W | 는 법선백터로 방향을 나타냄 |
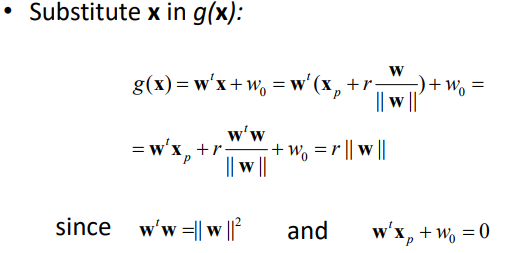
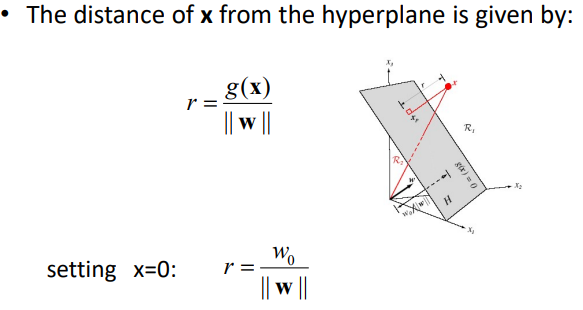
x 점을 g(x)에 대입해 보면 거리를 아래와 같이 정의할 수 있음
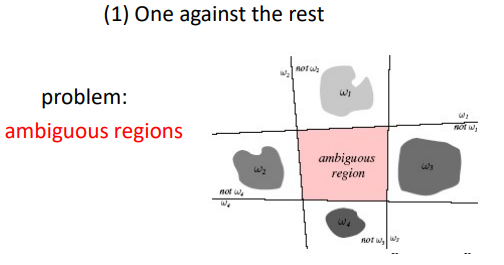
Linear Discriminant Fucntions:multi-category case
Linear 하게 접근할 때 아무것도 속하지 않거나 겹치는 ambiguous 한 부분 이 존재함
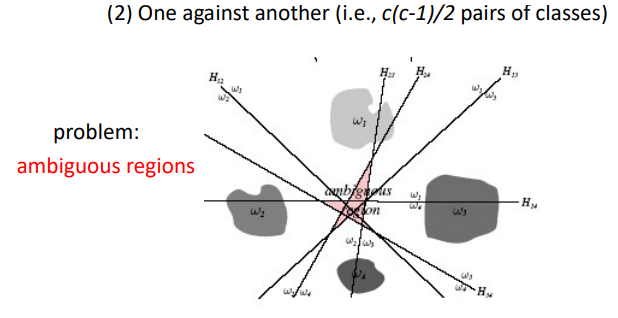
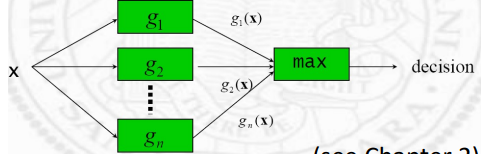
Linear Machine
이런 ambiguous regions을 피하기 위해 각 클래스에 대핸 분류기르 두고 여러 클래스 중 가장 큰 값으로 결정하는 것을 linear machine라 함
(One vs all)
linear machine 은 자르면 반드시 convex 영역으로 나누어진다
Convex 영역이란 영역속에서 임의의 두점을 연결할 때 영역 안에서 연결되어야함
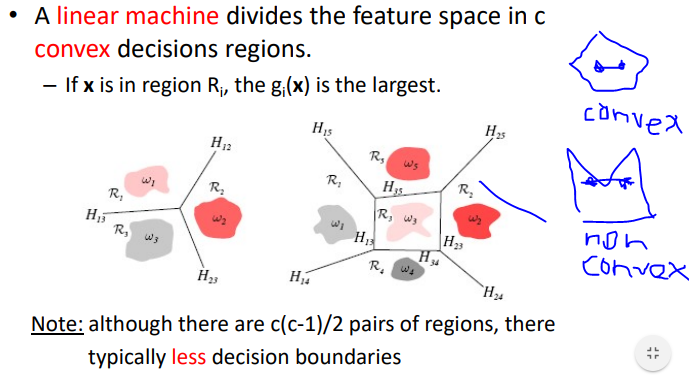
Higher Order Discriminant Functions
Linear가 차수가 낮고 간편한데 Classify 잘못함(XOR 같은 문제는 Linear로 해결 불가능)
Augmented feature/parameter space:
(일차방정식을 좀 더 Simple하게 만듬)
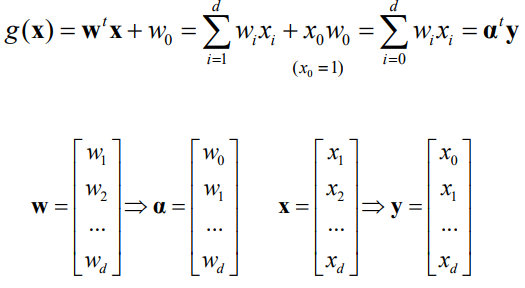
W0를 백터 안으로 넣고 X0는 항상 1임
Linear Regression의 가장 많이 쓰는 W^T*X 로 보면됨

위와 같은 문제로 간단히 변경될 수 있음
Generalized Discriminants
복잡한 것을 차원을 늘려 linearly seperable하게 변경해줌 -> Kernel function(∮을 이용함)

Example

위와 같은 문제는 선형적으로 해결하기 어려움
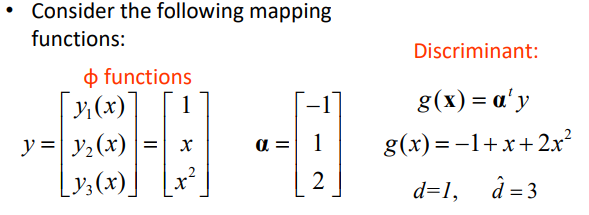
Kernel Function을 써서 차원을 높여 3차원으로 변경해줌
1차원 X -> 3차원 Y
여기서 a는 현재 어떻게 구하는지 아직 모름
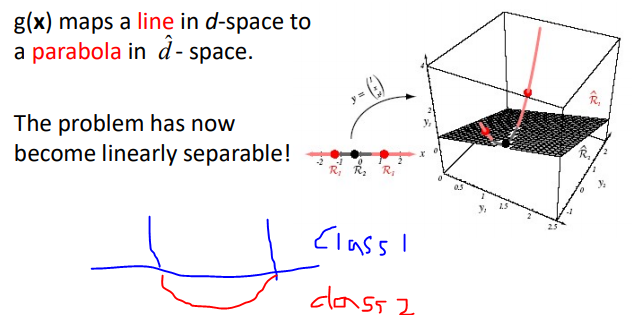
d여기서 weights 인 a를 구하는 것이 학습
a는 unique한 값이 아님
이 a를 찾는 것은 error function을 최소화 하는 a를 찾는 문제와 동일

-> Pk를 찾기위해 일반적으로 Gradient Descent를 이용
Initial에 따라 local minimum을 구할 수도 있고 Global minimum을 구할 수도 있음