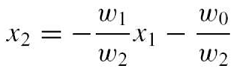Introduction to Neural Network
What is Neuron?
인간의 nerve system -> neuron
많은 수의 input을 받을 수 있고 단지 더해 out signal을 다른 뉴런으로 전파
매우 간단한 정보전달 시스템
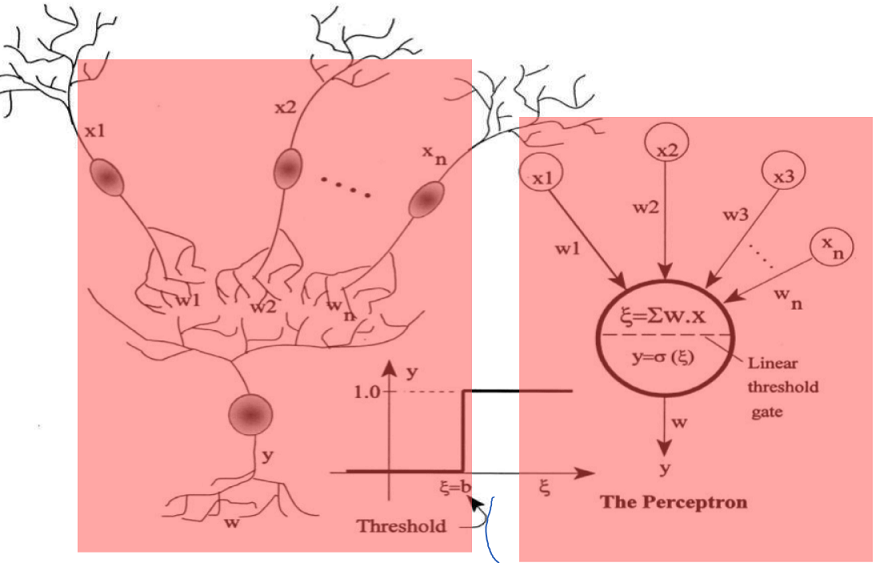
A neuron is an electrically excitable cell that processes and transmits information by electrical and chemical signaling
Biological -> Artificial Neural Network
생물학적 뉴런과 비슷하게 수학적으로 변경
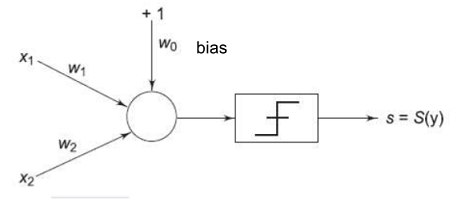
그림에서는 시그마 함수가 step function으로 되어 있어 b threshold 이상이면 1, 아니면 0임
이 시그마 함수가 시그모이드 함수 등으로 변경되는 것이 2세대 모델임
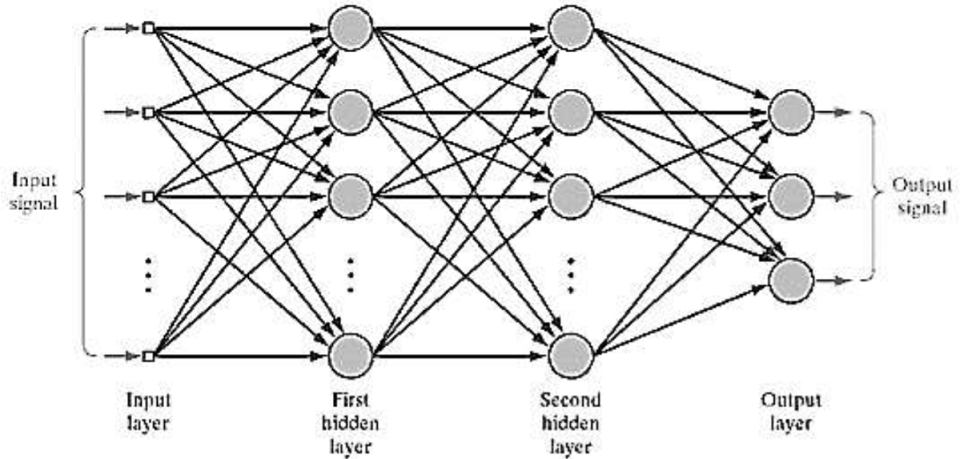
Artificial Neural Networks
인간의 뇌에 영감을 받아 정보를 처리하는 paradigm 임
각각의 뉴런들은 간단한 일 (다수의 신호를 입력으로 받아 하나의 신호를 출력)을 하지만 많은 수가 결합되면 복잡한 일이 가능함
각 뉴런들을 퍼셉트론이라하며 많은 퍼셉트론들을 결합하여 복잡한 일을 처리하도록 설계
Biological VS Artificial Neural Networks
인간은 10^10 뉴런들을 뇌에 가지고 있음
2017년 Intel이 Loihi라는 AI chip(Neuromorphic chip - 인간의 뇌를 흉내내기 위한 칩)을 개발
13000 뉴런들이 존재하며 130 million의 synapses(접합)을 가짐
Lobster’s의 뇌와 유사한 단계까지 옴
Pattern Classification
시각적인 요소를 이용해 sea bass 와 salmon을 구별해보는 것이 motivation
두 가지 물고기 사이에 육체적 특징의 다른점을 뽑으면 length, lightness, width, number and shape of fins… 등이 있을 것임
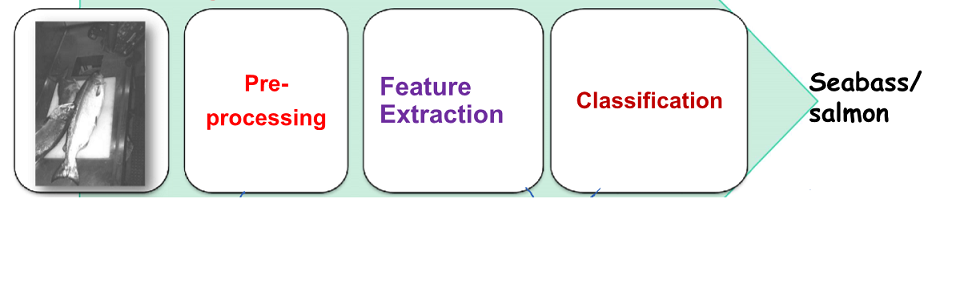
Pattern Recognition System
- Pre-processing : 도메인 지식이 필요
- Feature Extraction : 유용한 feature를 뽑음
- Classification : features을 평가해 물고기 타입을 결정
Feature Extraction과 Classification 이 ML에서 자동으로 찾을 수 있음
ML이 학습을 통해 Feature를 자동으로 찾고 분류 가능
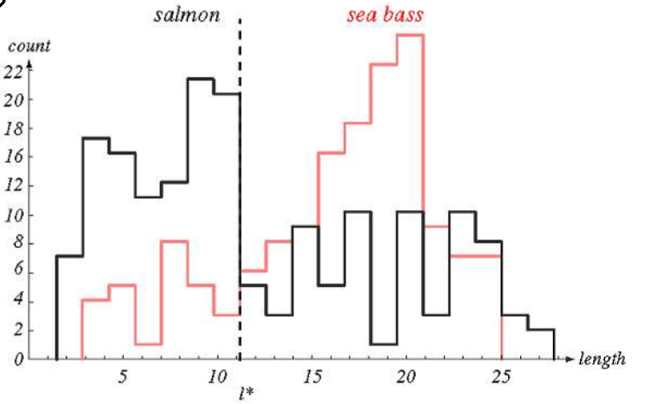
n 개의 Samples 들을 training data 로 가지고 length, lightness 각각의 Histograms으로 표현해봄
length Histogram
l* 점선이 합리적은 decision 인가?, 이 선을 어떻게 그을 것인가?
-> 이전 패턴인식 수업에서는 F1 Score 언급
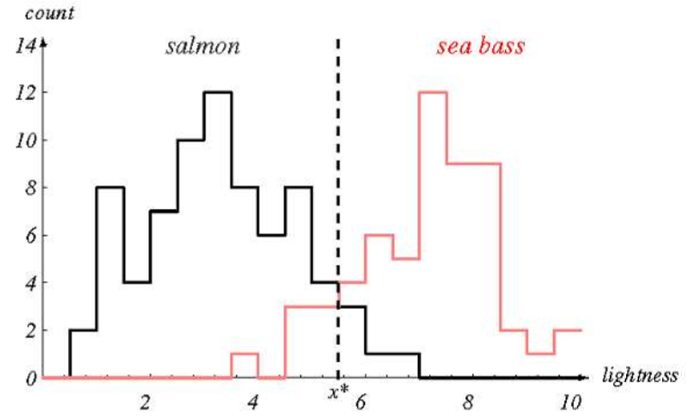
lightness Histogram
lightness 이 이전 length 보다 더 결정선을 결정하기 쉬움
but 완벽한 decision은 아님
패턴인식에서는 이렇게 좋은 feature를 뽑는 것이 중요함
하나의 feature만 쓰는 것보다 여러 feature를 결합 시켜 Classification 함(vector 로 표현)
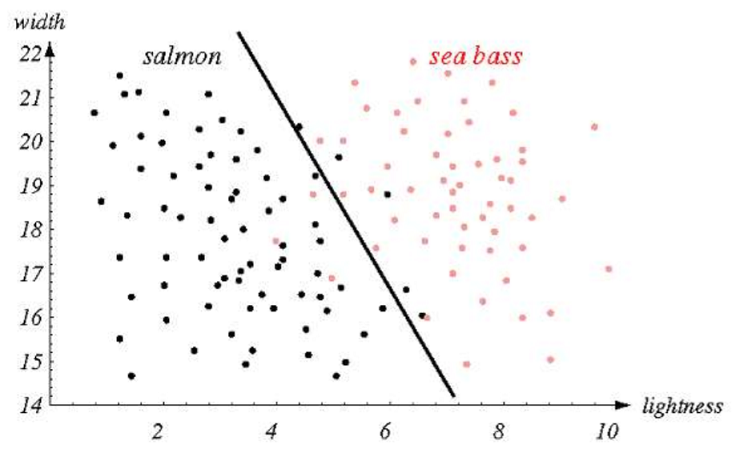
Using two features(Width, lightness)
Linear Decision으로 모든 것을 정확히 구분하기 어려움
Non-linear Decision Boundary 로 복잡해짐
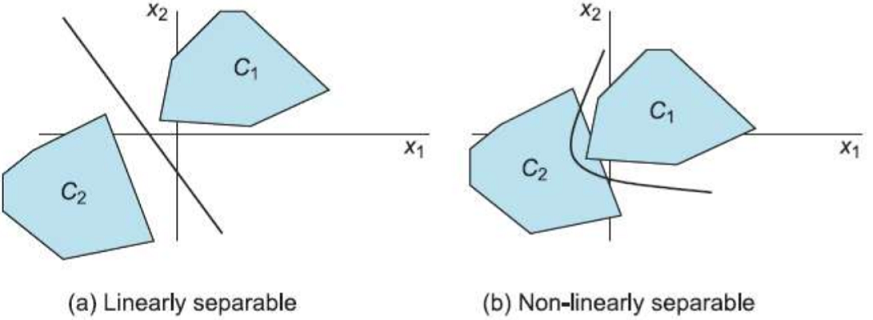
Non-linearly Separable Problems
하나의 hyperplane으로 나뉘면 linearly separable이라 부름
Perceptron
퍼셉트론은 다수의 신호를 입력으로 받아 하나의 신호를 출력
신호를 어떤 전류의 흐름이라 상상하면됨 (흐름을 만들고 정보를 앞을 전달)
Perceptrons are two-class classifier
실제 전류와 단리 퍼셉트론 신호는 흐른다 / 안흐른다 의 두가지 값을 가질 수 있음
- Input Vector : X = [1, x1, x2]
- Weight Vector : W = [w0, w1, w2]
- Internal bias : w0 with a constant + 1 input
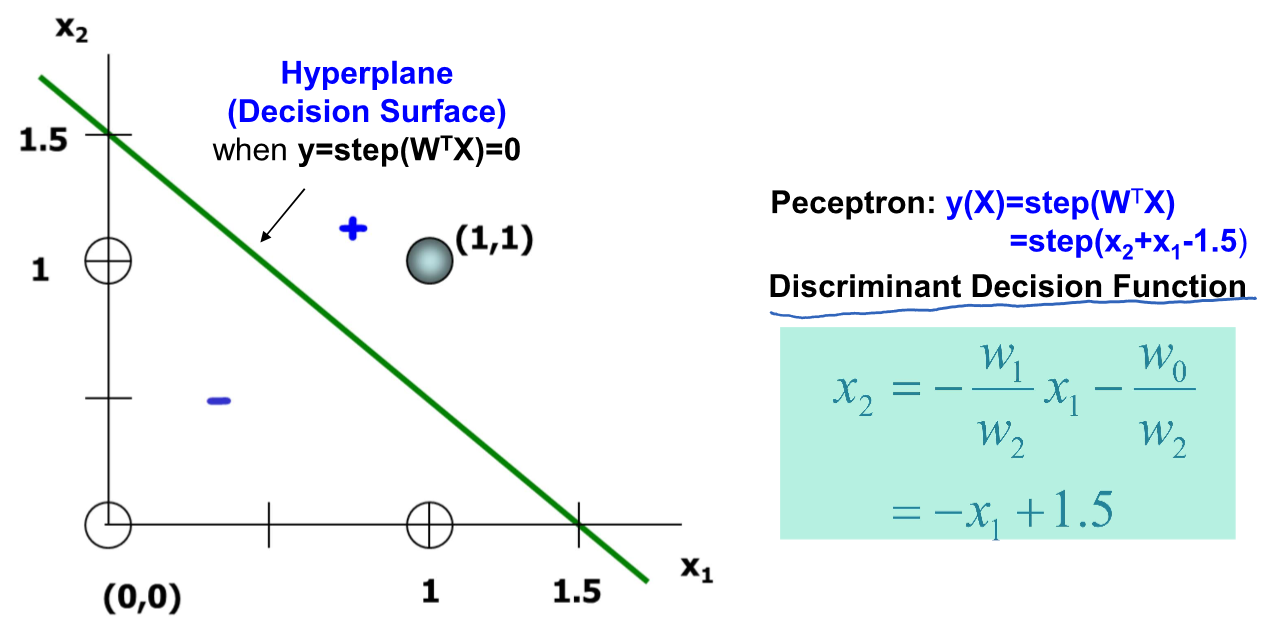
- Perceptronal activiation = y = step(X^T*W) = step(w1x1 + w2x2 + w0)
- Perceptron discriminant function(S) : y(X) = 0 if y>0, s=1 and if y<0, s=0
Discriminant Function
y(X) = W^T*X + w0 일 때 보통 2-class 문제에서는 y(X) >= 0 인 경우를 class1으로 분류하고 아닌경우 class 2로 분류
이때 결정 경계면은 y(X) = 0 임
만일 임의의점 Xa, Xb 가 경계면 위에 있다면
- y(Xa) = y(Xb) = 0
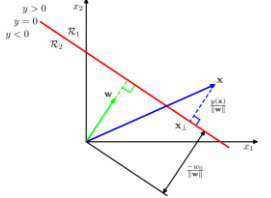
- y(Xa) - y(Xb) = 0 -> W^TXa - W^TXb = 0 -> W^T(Xa - Xb) = 0임을 만족하고 w는 결정 경계에 대해 orthogonal 함
따라서 inputs (x1, x2) 에 대한 결정함수는 w0 + w1x1 + w2x2 =0 이므로 아래와 같이 결정함수를 정할 수 있음
1개의 perceptron이 한개의 linear 한 hyperplane을 나타내고 복잡한 모형일 수록 perceptron 수가 많아짐